Zorba blog
RNN(Recurrnet Neural Neetwork) 본문
RNN의 등장배경
피드포워드 신경망의 문제점
- 단방향인 신경망이기 때문에 구성이 단순하여 구조를 이해하기 쉽고, 많은 문제에 응용할 수 있다는 장점이 있지만
- 시계열 데이터를 잘 다루지 못한다는 단점이 있음 -> 그래서 순환 신경망(RNN) 이 등장.
RNN(순환신경망) 이란
순환하는 신경망
- RNN의 특징은 순환하는 경로가 있다는 것.
- 이 순환 경로를 따라 데이터는 끊임없이 순환.
- 데이터가 순환되기 때문에 과거의 정보를 기억하는 동시에 최신 데이터로 갱신될 수 있음.

순환 구조 펼치기
- RNN 계층의 순환 구조를 펼침으로써 오른쪽으로 진행하는 피드포워드 신경망과 같은 구조.
- RNN에서는 다수의 RNN 계층 모두가 실제로는 '같은 계층'인 것이 피드포워드 신경망과의 차이점.
- 각 시각의 RNN 계층은 그 계층으로의 입력과 전의 RNN 계층으로부터의 출력을 받음. 그리고 이 두 정보를 바탕으로 현 시각의 출력을 계산.

- RNN에는 가중치가 2개 있음.
- 입력 x를 출력 h로 변환하기 위한 가중치 Wx.
- 1개의 RNN 출력을 다음 시각의 출력으로 변환하기 위한 가중치 Wh.
- ht는 다른 계층을 향해 위쪽으로 출력되는 동시에, 다음 시각의 RNN 계층을 향해 오른쪽으로도 출력.
Hyperbolic Tangent

- Hyperbolic tangent 함수는 Sigmoid 함수의 대체제로 사용될 수 있는 활성화 함수.
- Sigmoid와 비교하여 tanh는 출력 범위가 더 넓고 경사면이 큰 범위가 더 크기 때문에 더 빠르게 수렴하여 학습하는 특성.
RNN의 Backpropagation
BPTT(Backpropagation Through Time)

- 위의 그림에서 보듯이 순환 구조를 펼친 후의 RNN에는 피드포워드 오차역전파법을 적용할 수 있음.
- 즉, 먼저 순전파를 진행하고 이어서 역전파를 수행하여 원하는 기울기를 구할 수 있음.
- 여기서의 오차역전파법은 '시간 방향으로 펼친 신경망의 오차역전파법' 이라는 뜻으로 BPTT(Backpropagation Through Time)라고 함.
Truncated BPTT
- 시계열 데이터의 식나 크기가 커지는 것에 비례하여 BPTT가 소비하는 컴퓨팅 자원도 증가.
- 또한 시간 크기가 커지면 역전파 시에 기울기 값이 조금씩 작아져서 0에 가까워지는 문제도 발생.
*Vanishing Gradient Problem : 신경망을 통과할 때마다 기울기 값이 조금씩 작아져서 0에 가까워지는 문제.
- 이런 문제를 해결하기 위해 신경망 연결을 적당한 길이로 '끊는다'.
- 시간축 방향으로 너무 길어진 신경망을 적당한 지점에서 잘라내 여러 개로 만든다는 아이디어

- Truncated BPTT에서는 신경망의 연결을 끊지만, 제대로 구현하려면 '역전파'의 연결만 끊고, '순전파'의 연결은 반드시 그대로 유지 해야함. 즉, 순전파의 흐름은 끊어지지 않고 전파.
- 길이가 1,000인 시계열 데이터가 있다고 가정. RNN 계층을 펼치게 되면 계층이 가로로 1,00개나 늘어선 신경망.
- 순전파의 연결은 유지한 채 역전파의 연결만 적당한 지점에서 끊음.
- 각각의 블록 단위로, 미래의 블록과는 독립적으로 오차역전파법을 완성.

- 위의 그림처럼 Truncated BPTT에서는 데이터를 순서대로 입력해 학습.
- 이런 식으로 순전파의 연결을 유지하면서 블록 단위로 오차역전파법을 적용.
RNN 구현
RNN 계층
- 구현해야 할 것은 결국 가로 방향으로 성장한 신경망.
- Truncated BPTT 방식의 학습을 따른다면, 가로 크기가 일정한 일련의 신경망.
- 우리가 다룰 신경망은 길이가 T인 시계열 데이터를 입력으로 받고, (T는 임의의 값), 각 시각의 Hidden State(은닉 상태)를 T개 출력.
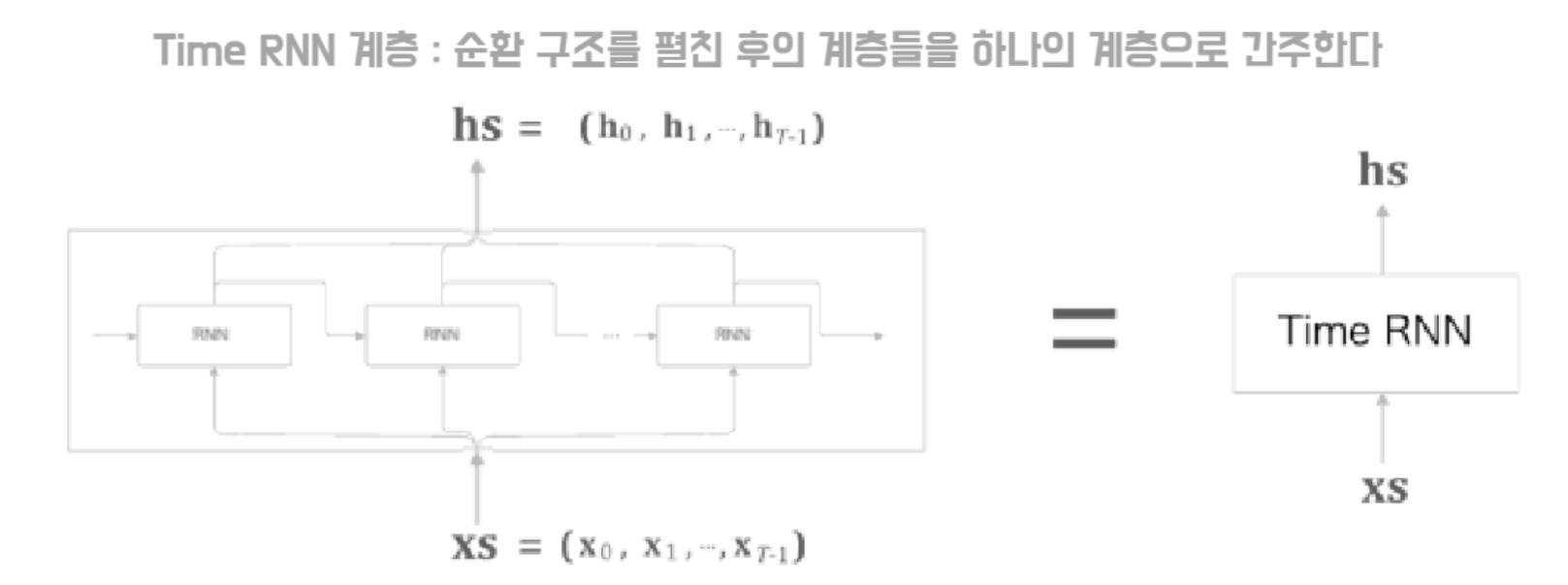
- 먼저 RNN 한 단계를 처리하는 클래스를 RNN이란 이름으로 구현.
- 이 RNN 클래스를 이용하여 T개 단계의 처리를 한꺼번에 수행하는 계층을 TimeRNN이란 이름의 클래스로 완성.
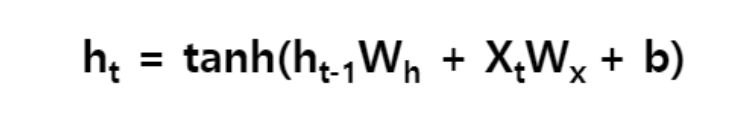
- 데이터를 미니배치로 모아서 처리.
- 계산할 데이터의 형상 확인.(미니배치 크기가 N, 입력 벡터의 차원수가 D, 은닉 상태 벡터의 차원수가 H)
RNN 계층의 순전파

__init__()
- RNN의 초기화 메서드는 가중치 2개와 평향 1개를 인수로 받음.
- 인수로 받은 매개변수를 인스턴스 변수 params에 리스트로 저장.
- 각 매개변수에 대응하는 형태로 기울기를 초기화한 후 grads에 저장.
- 마지막으로 역전파 계산 시 사용하는 중간 데이터를 담을 cache를 None로 초기화.
forward()
- 순전파인 forward 메서드는 입력 x와 이전 층의 h_prev를 인수로 받음.
- 그 다음은 RNN 계층의 계산 그래프 상의 과정을 코드로 옮긴 것.
RNN 계층의 역전파
(1) dh(next)

backward()
- backward()는 다음 층의 역전파인 dh_next를 인수로 받음.
- __init__()에서 역전파 계산을 위해 미리 저장해놓은 cache 변수로부터 x, h_prev, h를 받아옴.
(2) dtanh

backward()
- tanh의 미분 계산에 따라 dtanh를 계산.
(3) 덧셈 노드

backward()
- 역전파를 그대로 흘려보냄.
- 여기서는 미니배치 단위 학습을 고려해서 만든 코드이므로 db는 NxH의 형상이라고 고려.
- 편향의 역전파는 데이터를 단위로 한 축인 axis=0의 총합을 구함.
(4) 곱셈 노드

backward()
- 상류에서 들어온 값에 순전파 때의 입력 신호들을 '서로 바꾼 값'을 곱하면 됨.
'Machine Learning' 카테고리의 다른 글
| Convolutional Neural Network(CNN) (0) | 2022.08.06 |
|---|---|
| LSTM and GRU(Long Short Term Memory & Gated Recurrent Unit) (0) | 2022.08.06 |
| Gradient Descent Optimization Algorithms (0) | 2022.06.23 |
| 앙상블(Ensemble) / Bagging, Boosting, Stacking (0) | 2022.06.22 |
| 서포트 벡터 머신 (Support Vector Machine, SVM) (0) | 2022.05.16 |


