Zorba blog
트랜스포머(Transformer) 모델 / 인코더, 포지션-와이즈 피드 포워드 신경망, 잔차 연결, 정규화 본문
6. 인코더(Encoder)

- 트랜스포머는 num_layers 개수의 인코더 층을 쌓음.
- 인코더를 하나의 층이라고 생각한다면, 하나의 인코더 층은 총 2개의 서브층으로 나뉘어짐.
1) 셀프 어텐션 2) 피드 포워드 신경망
7. 인코더의 셀프 어텐션
1) 셀프 어텐션의 의미와 이점
- 어텐션 함수는 주어진 '쿼리(Query)' 에 대해서 모든 '키(Key)' 와의 유사도를 각각 구함.
- 구해낸 이 유사도를 가중치로 하여 키와 맵핑되어있는 각각의 '값(Value)'에 반영.
- 그리고 유사도가 반영된 '값(Value)'을 모두 가중합하여 리턴.
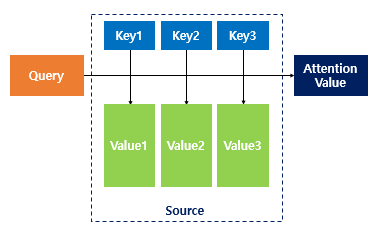
- 여기까지는 이전에 학습한 어텐션의 개념. 셀프 어텐션과의 차이는? 셀프 어텐션은 어텐션을 자기 자신에게 수행.
- seq2seq에서 어텐션을 사용할 경우의 Q,K,V의 정의를 다시 보면, 그리고 t시점을 전체 시점으로 일반화하면?
- 이처럼 디코더 셀의 은닉 상태가 Q이고 인코더 셀의 은닉 상태가 K라는 점에서 Q와 K가 서로 다른 값을 가짐.
| Q = Query : t 시점의 디코더 셀에서의 은닉 상태 / 모든 시점의 디코더 셀에서의 은닉 상태들 K = Keys : 모든 시점의 인코더 셀의 은닉 상태들 / 모든 시점의 인코더 셀의 은닉 상태들 V = Values : 모든 시점의 인코더 셀의 은닉 상태들 / 모든 시점의 인코더 셀의 은닉 상태들 |
- But. 셀프 어텐션에서는 Q, K, V가 전부 동일.
| Q = 입력 문장의 모든 단어 벡터들 K = 입력 문장의 모든 단어 벡터들 V = 입력 문장의 모든 단어 벡터들 |

- 위 그림처럼 셀프 어텐션은 입력 문장 내의 단어들끼리 유사도를 구하므로서 그것(it)이 동물(animal)과 연관되었을 확률이 높다는 것을 찾아냄.
- 아래에서부터 셀프 어텐션의 동작 메커니즘.
2) Q, K, V 벡터 얻기
- 셀프 어텐션은 인코더의 초기 입력인 dmodel의 차원을 가지는 단어 벡터들을 사용하여 셀프 어텐션을 수행하는 것이 아니라 우선 각 벡터들로부터 Q, K, V 벡터를 얻는 작업을 거침.
- 이 Q, K, V 벡터들은 초기 입력인 dmodel의 차원을 가지는 단어 벡터들보다 더 작은 차원을 가짐.
- 논문에서는 dmodel=512의 차원을 가졌던 각 단어 벡터들을 64의 차원을 가지는 Q, K, V 벡터로 변환.
- 64라는 값은 트랜스포머의 하이퍼파라미터 num_heads로 인해 결정. dmodel/num_heads 값이 Q,K,V 벡터 차원.
(논문에서 num_heads의 값은 8, 512/8=64)
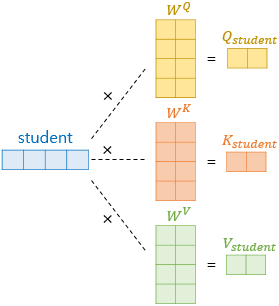
- 기존의 단어 벡터에 가중치 행렬을 곱하여 더 작은 벡터 완성.
- 각 가중치 행렬은 dmodel x (dmodel/num_heads)의 크기를 가짐. ( 512 x (512/8) = 512 x 64 행렬 )
- 이 가중치 행렬은 훈련 과정에서 학습.
- 각 단어 벡터에 3개의 서로 다른 가중치 행렬을 곱하고 64의 크기를 가지는 Q, K, V 벡터를 얻음.
- 즉, dmodel 차원을 가졌던 한 토큰의 벡터는 각각의 가중치 행렬을 곱하여 dmodel/num_heads 차원의 벡터로으로 변환
3) 스케일드 닷-프로덕트 어텐션(Scaled dot-product Attention)
- Q, K, V 벡터를 얻었다면 기존에 배운 어텐션 메커니즘과 동일.
- 각 Q벡터는 모든 K벡터에 대해서 어텐션 스코어(Attention Score)를 구하고, 어텐션 분포를 구한 뒤에 이를 사용하여 모든 V벡터를 가중합하여 어텐션 값 또는 Context Vector를 구함.
- 기존에는 내적만을 사용하는 어텐션 함수(score(q,k)=q·k)였지만, 여기에 특정값으로 나눠준 아래의 어텐션 함수를 사용.
함수 입력
- 기존 닷-프로덕트 어텐션(dot-product attention)에서 값을 스케일링하는 것을 추가하였다고 하여 스케일드 닷-프로덕트 어텐션(Scaled dot-product Attention) 이라고 함.
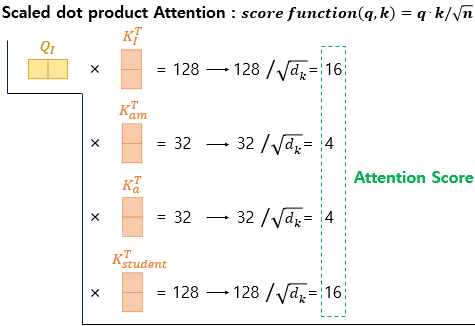
- 논문에서 dk의 값은 dmodel/num_heads라는 식에 따라 64의 값을 가지므로 분모는 8의 값을 가지게 됨.

- 이제 이전처럼 소프트맥스 함수를 사용하여 어텐션 분포(Attention Distribution)을 구하고,
각 V벡터와 가중합하여 어텐션 값(Attention Value)을 구함.
- 이는 단어 I에 대한 어텐션 값 or 컨텍스트 벡터(Context Vector)라고도 할 수 있음.
- 이 과정을 am, a, student에 대해서도 동일하게 반복해야 하는데, 행렬 연산으로 일괄 처리할 수 있음.
4) 행렬 연산으로 일괄 처리하기
- 각 단어에 대해 Q, K, V 벡터를 구하고 스케일드 닷-프로덕트 어텐션을 수행하였던 위 과정들을 행렬 연산으로 처리 가능.
- 각 단어 벡터마다 일일히 가중치 행렬을 곱하는 것이 아니라 문장 행렬에 가중치 행렬을 곱하여 Q, K, V 행렬을 구함.

- I am a student 는 4 x 512 행렬을 가지고, 가중치 행렬 W는 512 x 64, Q,K,V 행렬은 4 x 64 shape을 가짐.
(dmodel=512, num_heads=8)
- 이를 통해 각 토큰의 Q, K, V 벡터값을 가지는 행렬을 구할 수 있음

- 이제 Q와 K의 스케일드 닷-프로덕트를 수행하기 위해 Q행렬에 전치한 K행렬을 곱하고, 전체적으로 root(dk) 로 나눔.
- 각 행과 열은 어텐션 스코어를 가지는 행렬이 됨.
- 이제 남은 것은 어텐션 분포(Attention Distribution)을 구하고, 소프트맥스 함수를 사용한 뒤, V행렬을 곱하는 것.
- 어텐션 스코어 행렬에 행 단위로 소프트맥스 함수를 적용하고, V행렬에 곱하면 어테션 값 행렬이 결과로 나옴.

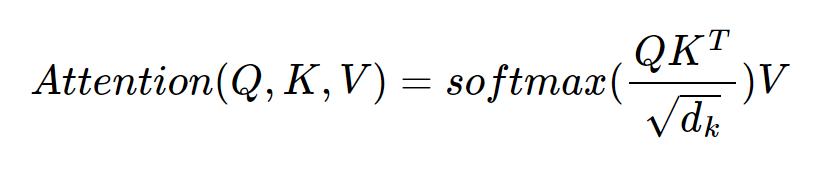
- 행렬의 크기 정리. 입력 문자의 길이를 seq_len. 문장 행렬의 크기는(seq_len, dmodel)
- Q벡터와 K벡터의 차원을 dk라 하고, V벡터의 차원을 dv라고 해보자.
- Q행렬과 K행렬의 크기는 (seq_len, dk) 이며, V행렬의 크기는 (seq_len, dv).
- Wq, Wv는 (dmodel, dk)의 크기를 가지며, Wv는 (dmodel, dv)의 크기를 가짐.
(단 논문에서는 dk, dv의 차원은 dmodel/num_heads와 같음)
- 결과적으로 어텐션 값 행렬의 크기는 (seq_len, dmodel/num_heads)이 됨.
5) 멀티 헤드 어텐션(Multi-head Attention)
- 지금까지 dmodel의 차원을 가진 단어 벡터를 num_heads로 나눈 차원을 가지는 Q,K,V 벡터로 바꾸고 어텐션을 수행.
- num_heads의 의미와 왜 dmodel의 차원을 가진 단어 벡터를 차원을 축소시킨 벡터로 어텐션을 수행하였는지 확인.

- 트랜스포머 연구진은 한 번의 어텐션 보다 여러번의 어텐션을 병렬로 수행하는 것이 더 효과적이라고 판단.
- 그래서 dmodel의 차원을 num_heads개로 나누어 dmodel/num_heads의 차원을 가지는 Q,K,V에 대해서 num_heads개의 병렬 어텐션 수행.
- 이때 가중치 행렬 Wq,Wk,Wv의 값은 8개의 어텐션 헤드마다 전부 다름.
- 어텐션을 병렬로 수행함으로써 다른 시각으로 정보들을 수집.
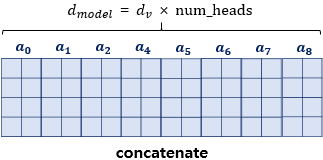
- 병렬 어텐션을 모두 수행하였다면 모든 어텐션 헤드를 연결(concatenate).
- 모두 연결된 어텐션 헤드 행렬의 크기는(seq_len, dmodel)가 됨. (4 x 64 *8) = (4 x 512)

- 멀티-헤드 어텐션의 최종 결과물은 concatenaed matrix 와 또 다른 가중치 행렬 W를 곱한 것.
- 이때 결과물은 인코더의 입력이었던 (seq, dmodel) 크기와 동일. (4 x 512)
- 인코더의 첫번째 서브층인 멀티-헤드 어텐션 단계를 끝마쳤을 때, 인코더의 입력으로 들어왔던 행렬의 크기가 유지.
- 두번째 서브층인 포지션 와이즈 피드 포워드 신경망을 지나도 행렬의 크기를 계속 유지.
- 인코더에서의 입력의 크기가 출력에서도 동일 크기로 계속 유지되어야만 다음 인코더에서도 다시 입력이 될 수 있음.
6) 패딩 마스크(Padding Mask)
- 스케일드 닷 프로덕트 어텐션 함수 내부를 보면 mask라는 값을 인자로 받아서,
이 mask에다가 -1e9라는 아주 작은 음수값을 곱한 후 어텐션 스코어 행렬에 더해줌.
- 이 연산의 정체는?
def scaled_dot_product_attention(query, key, value, mask):
... 중략 ...
logits += (mask * -1e9) # 어텐션 스코어 행렬인 logits에 mask*-1e9 값을 더해주고 있다.
... 중략 ...- 이는 입력 문장에 <PAD> 토큰이 있을 경우 어텐션에서 사실상 제외하기 위한 연산.
- 아래는 <PAD>가 포함된 입력 문자의 셀프 어텐션의 예제.

- 단어 <PAD>의 경우 실질적인 의미를 가진 단어가 아님.
- 트랜스포먼에서는 Key의 경우에 <PAD> 토큰이 존재한다면 이에 대해서는 유사도를 구하지 않도록 마스킹 추가.
- 어텐션 스코어 행렬에서 행에 해당하는 문장은 Query이고, 열에 해당하는 문장은 Key.
- Key에 <PAD>가 있는 경우 해당 열 전체를 마스킹.

- 마스킹을 하는 방법은 행렬의 마스킹 위치에 매우 작은 음수값을 넣는 것.(-1,000,000,000과 같은 -무한대)
- 아직 어텐션 스코어 함수는 소프트맥스 함수를 지나지 않음.
- 현재 마스킹 위치에 매우 작은 음수 값이 들어가 있으므로 어텐션 스코어 행렬이 소프트맥스 함수를 지난 후에는 해당 위치의 값은 0이 되어 단어 간 유사도를 구하는 일에 <PAD> 토큰 반영 X

- 소프트맥스 함수를 지난 후의 어텐션 스코어 행렬. 단어 <PAD>의 경우에는 0이 되어 어떤 유의미한 값을 가지지 않음.
8. 포지션-와이즈 피드 포워드 신경망(Position-wise FFNN)
- 포지션-와이즈 FFNN은 인코더와 디코더에서 공통적으로 가지고 있는 서브층.


- 여기서 x는 앞서 멀티 헤드 어텐션의 결과로 나온 (seq_len, dmodel)의 크기를 가지는 행렬.
- 가중치 행렬 W1은 (dmodel, dff)의 크기를 가지고, W2는 (dff, dmodel)의 크기를 가짐.
(논문에서 은닉층의 크기인 dff는 2,048로 설정)
- W1,b1,W2,b2는 하나의 인코더 층 내에서는 다른 문장, 다른 단어들마다 정확하게 동일하게 사용.
- 하지만 인코더 층마다는 다른 값을 가짐.

- 두 번째 층을 지난 인코더의 최종 출력은 여전히 인코더의 입력의 크기였던 (seq_len, dmodel)의 크기가 보존.
9. 잔차 연결(Residual connection) 과 층 정규화(Layer Normalization)

- 트랜스포머에는 이러한 두 개의 서브층을 가진 인코더에 추가적으로 Add & Norm 기법 사용.
- 정확히는 잔차 연결(Residual connection) 과 층 정규화(layer normalization)을 의미.
1) 잔차 연결(Residual connection)
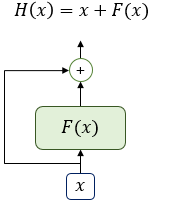
- F(x)가 트랜스포머에서는 서브층에 해당.
- 잔차 연결은 서브층의 입력과 출력을 더하는 것을 의미.
- 트랜스포머에서 서브층의 입력과 출력은 동일한 차우너을 갖고 있으므로, 서브층의 입력과 서브층의 출력은 덧셈 연산을 할 수 있음.


2) 층 정규화(Layer Normalization)
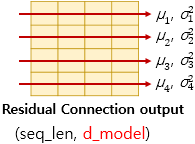
- 잔차 연결을 거친 결과는 이어서 층 정규화 과정을 거치게 됨.
- 잔차 연결의 입력을 x, 잔차 연결과 층 정규화 두 가지 연산을 모두 수행한 후의 결과 행렬을 LN이라고 하면 수식은 아래과 같음.

- 층 정규화는 텐서의 마지막 차원에 대해서 평균, 분산을 구하고 이를 가지고 값을 정규화하여 학습을 도움.
- 여기서 텐서의 마지막 차원이란 것은 트랜스포머에서는 dmodel 차원을 의미.
- 층 정규화를 두 가지 과정으로 나누어서 설명.
- 첫 번째는 평균과 분산을 통한 정규화, 두 번째는 감마와 베타를 도입.
- 우선 평균과 분산을 통해 벡터 xi를 정규화.

- 입실론은 분모가 0이 되는 것을 방지.
- 이제 감마와 베타라는 벡터를 준비. 이들의 초기값은 각각 1과 0.

- 층 정규화의 최종 수식은 다음과 같으며 감마와 베타는 학습 가능한 파라미터.
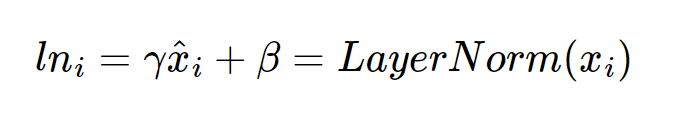
'자연어처리' 카테고리의 다른 글
| 버트(Bidirectional Encoder Representations from Transformers, BERT) (0) | 2022.06.07 |
|---|---|
| NLP에서의 사전 훈련(Pre-Training) (0) | 2022.06.03 |
| 트랜스포머(Transformer) 모델 / 개념, 포지셔널 인코딩(Positional Encoding) (0) | 2022.06.02 |
| 어텐션 메커니즘 (Attention Mechanism) (0) | 2022.05.31 |
| 시퀀스-투-시퀀스(Sequence-to-Sequence, seq2seq) (0) | 2022.05.31 |




